（推定読了時間：41分40秒）

2015年12月17日、Google Chrome の JavaScript エンジン（処理系）である V8 の公式ブログにて、 JavaScript の標準的な乱数生成APIである Math.random() の背後で使われているアルゴリズムの変更がアナウンスされました。 Math.random() 関数は JavaScript を利用する際には比較的よく使われる関数ですので、親しみのある方も多いのではないかと思います。

新たなバグの発見や、従来より優秀なアルゴリズムの発見によってアルゴリズムが変更されること自体はそれほど珍しくはないものの、 技術的には枯れていると思われる Math.random() のような基本的な処理の背後のアルゴリズムが変更されたことに驚きを感じる方も少なくないかと思いますが、 それ以上に注目すべきはその変更後のアルゴリズムです。

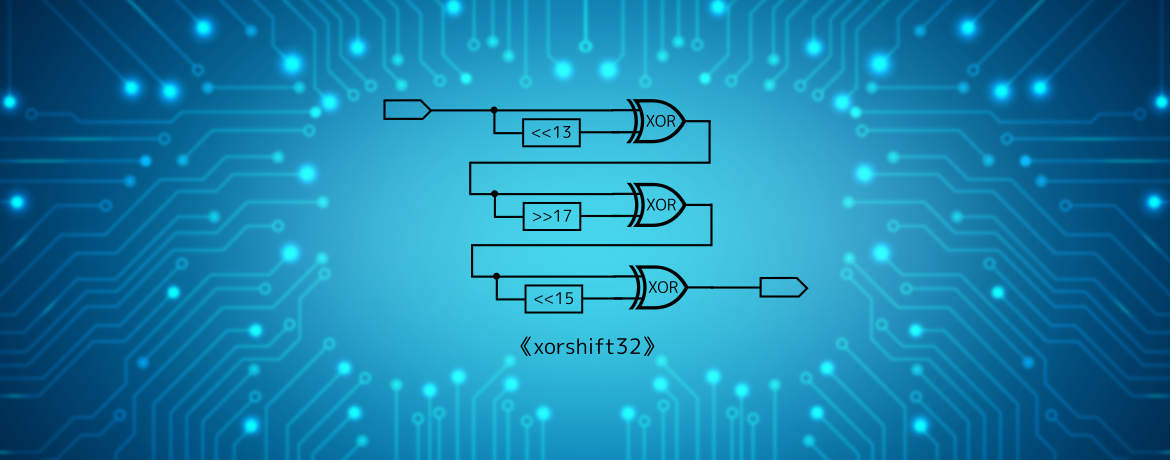
実際に採用されたアルゴリズムの原型となるアルゴリズムは xorshift32（xorshift は様々なビット数のバージョンがあり、そのうちの32ビット版のこと）と呼ばれる以下の処理です。

上のコードをご覧いただけるとわかる通り、ビットシフトとXOR (排他的論理和) だけからなる非常に簡単な処理をたった三回行うだけの、非常にシンプルな処理となっております。 しかしながら、このような非常に単純な処理で本当に「良い」乱数を生成することができるのでしょうか？

「同じような値が出続けることはないの？」「ちゃんと一様な乱数になってるの？小さい値に偏ったりしないの？」 「どんな初期値を入れても大丈夫なの？」「てか、13とか17とか15とかいう数字は何処から？」などなど、疑問ばかり出てます。

ところが、処理の簡素さとは裏腹に、上のコードの「シフトしてから元の値とXORをとる」という処理は非常に巧妙に出来ていて、 実はきちんと数学的な解析を行うことにより様々な「良い性質」を持つ処理であることが証明できてしまうのです！

そこで本記事では、上記の xorshift32 というアルゴリズムが「良い性質」を持つ乱数生成アルゴリズムであることの、数学的な解析を行います。

本記事の内容は xorshift の発明者である George Marsaglia 氏による論文に基づきます。

なお、本記事を読むにあたり行列同士の掛け算や、行列・ベクトル積の計算方法などの基本的な知識があることを仮定しています。 より深く理解するためには大学初年度程度の線形代数や群論などの知識があることが望ましいですが、 数学にそれほど明るくないプログラマの方でも理解できるよう、なるべく平易に書いたつもりですので、あまり臆せずに読み進んでいただけたらと思います。

擬似乱数の性質

擬似乱数の良し悪し

さて、突然ですが問題です。

「性質の良い擬似乱数」とはどのような性質をみたす擬似乱数のことでしょうか？

近い値がやたら連続して出ないこと？偶数と奇数がほぼ交互に出現すること？次に出る乱数と、その一つ前の乱数に単純な関係がないこと？ 小さい値ばかりに偏って出てこないこと？二進数表示にした時に、”0″と”1″の出現確率がそれぞれ 0.5 ずつであること？

……などなど、他にもいろいろと考えられると思います。

では正解は何かというと、そんなものはありません。いえ、強いて言うならば、上に挙げた性質と、読者の方が挙げた性質すべてです。

非常に歯切れの悪い言い方ですが、実は与えられた数列が乱数かどうかを判定するのは非常に難しく、 「この性質があれば乱数とみなしても良い」と断言できるようなものはありません。

しかしながら上に挙げたような「乱数であればこんな性質を満たすだろう」というものはたくさん考えることができますので、 そういった性質をみたすかどうかを一つづつチェックしていき、どのくらいテストに合格するかどうかで「乱数の良さ」を判定するということを行うというのが一般的です。 ただ、計算機で一定の手続きを用いて計算した擬似乱数（≠真の乱数）がこれらすべての性質をみたすことはあり得ませんから、 まぁ少しくらい当てはまらないものがあっても良しとしてしまっているのが現状です。 （例えば、擬似乱数生成アルゴリズムとして非常によく使われる Mersenne Twister も、すべての乱数テストには合格しません。）

ちなみに、有名な乱数テスト（をいくつか集めたスイート）として「Diehard」「TestU01」などがあります。

擬似乱数の周期

さて、「乱数っぽい性質」にはいくつもの種類があるのですが、その中でも最も基本的で、およそすべての擬似乱数生成アルゴリズムが満たすべき性質として「周期が非常に長いこと」というものがあげられます。

ここで「擬似乱数の周期」とは何かというと、擬似乱数生成アルゴリズムには必ず内部的な状態（この内部状態の初期値はいわゆる「シード値」と呼ばれます）があるのですが、 この内部状態は有限の範囲しかとりませんので、何度も繰り返し擬似乱数を作っていると必ず内部状態が一番初めのもの[1]に戻ってきてしまいます。 この、内部状態が初めの状態に戻ってきてしまうまでの回数のことを「擬似乱数の周期」といいます。

あまり周期が短いと、何度も繰り返し擬似乱数を生成しているうちに全く同じ数列が出てきてしまうことになるため、これではとても乱数とは言い難いです。 そもそも出力が32ビットなのに $2^{32}$ 以下の周期しかないということは、乱数として絶対に出てこない数があるということですので、こういった点でも乱数として失格です。

ですので一般に、擬似乱数の周期は長ければ長いほど良い擬似乱数であるといえるでしょう[2]。 例えば Mersenne Twister はライブラリの中などでは MT19937 と呼ばれることがあるのですが、この 19937 という数字は Mersenne Twister のもつ周期が $2^{19937}-1$ であることを示しており、このような非常に長い周期を持つことが Mersenne Twister の人気の理由の一つとなっています[3]。

それでは冒頭にソースコードを掲げた xorshift32 の場合の周期はどのくらいなのでしょうか？ 処理が非常に単純ですから、シード値を慎重に選ばないと短い周期になってしまいそうな気がしますし、最も周期が長くなるシード値を見つけ出すことができたとしても、 はたして Mersenne Twister 顔負けの非常に長い周期になってくれるのでしょうか……？

ところがこのような懸念とは裏腹に、線形代数や行列の知識（と、ほんの少しの数値計算）を駆使することで、xorshift32 というアルゴリズムが $2^{32}-1$ という非常に長い周期を持つことを数学的に示すことができるのです！ 特に、xorshift32 が内部状態としてもつ変数である y は 32 ビットの整数であり、これは高々 $2^{32}$ 種類の異なる値しか取ることはできませんので、 $2^{32}-1$ という周期を持つということは、ほぼ最も長い[4]周期を持っていることがわかります。

以降の節では、xorshift32というアルゴリズムが $2^{32}-1$ という周期を持つことの数学的な証明を目標として議論を進めていきます。 少し難しい数学的な概念がいくつか出てきますが、丁寧に議論を追っていけば理解できるものだと思いますので、 数学があまり得意でないプログラマの方も諦めずにぜひチャレンジしてもらえればと思います。

行列・ベクトル表現

まずは XOR やビットシフトと言った計算機的な操作を数学的に扱いやすくするために、数学的な言葉で置き換えてみましょう。 特に数学では扱う対象を行列やベクトルで表すことが多いですので、ここでも変数であったり XOR やビットシフトなどの操作を行列やベクトルの言葉で書きなおしてみます。

なお、ここでは説明の簡便さのために、すべて4ビットの変数に関する議論をしていますが、32ビットや64ビットでもほぼ同様の結果が成り立つことに注意してください。

ビット列のベクトル表現

まず変数（整数）ですが、これは二進数表記のビット列に変換してから、一番目のビットを一行目、二番目のビットを二行目、といった具合においたベクトルで表現することにしましょう[5]。 例えば x = 0b1100（先頭の「0b」は、以降の数値が二進数表記のものであることを示しています）という4ビット整数は、 \[ x = \begin{bmatrix} 1 \\ 1 \\ 0 \\ 0 \end{bmatrix} \] というベクトルで表現することにします。 このようなベクトルを（ベクトルの各要素は 0, 1 のみの二進数＝バイナリなので）「バイナリベクトル」と呼びます。 ただし、ベクトルの各行は1ビット整数ですので、ベクトル同士の足し算などを行った結果も1ビットの整数に丸めて（桁溢れした分は無視して）表現します。 例えば、 \[ \begin{bmatrix} 1 \\ 1 \\ 0 \\ 0 \end{bmatrix} + \begin{bmatrix} 1 \\ 0 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ 1 \\ 0 \end{bmatrix} \] といった具合です。 一行目は 1 + 1 = 2 = 0b10 ですが、2ビット目以降の数字は桁溢れとして無視しますので、最終的な結果は 1 + 1 = 0 となっています。

さて、ここで一つ注目してほしいことがあるのですが、1ビット同士の足し算の様子を表にすると

x y x + y
0 0 0
0 1 1
1 0 1
1 1 0

となりますが、これを真理値表と思うと、なにか見覚えがないでしょうか……？ 実はこれは x ^ y (x XOR y) と全く同じ真理値表となっています。

x y x ^ y
0 0 0
0 1 1
1 0 1
1 1 0

すなわち、上のように数値をベクトル表記した場合の足し算と、数値同士を XOR を取るという操作は全く同じものであるということです。 従って \[ \begin{bmatrix} 1 \\ 1 \\ 0 \\ 0 \end{bmatrix} + \begin{bmatrix} 1 \\ 0 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ 1 \\ 0 \end{bmatrix} \] という式は、計算機的には \[ 0b1100 \text{ ^ } 0b1010 = 0b0110 \] という計算をしていることと等価となります。

なんとなく xorshift の前半部分の xor が出てきましたね。 残るは後半部分の shift（ビットシフト）です。

ビットシフトの行列表現

ビットシフトについては行列（「バイナリ行列」という）の掛け算で表現することができます。 例えば 1 ビットの左シフトであれば、 \[ L_1 := \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} \] という行列で表されます。 実際、0b1011（に対応したベクトル）をこの行列に対して掛け算すると、 \[ \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 0 * 1 + 1 * 0 + 0 * 1 + 0 * 1 \\ 0 * 1 + 0 * 0 + 1 * 1 + 0 * 1 \\ 0 * 1 + 0 * 0 + 0 * 1 + 1 * 1 \\ 0 * 1 + 0 * 0 + 0 * 1 + 0 * 1 \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ 1 \\ 0 \end{bmatrix} \] ですので、確かに 0b1011 を 1 ビット左シフトした 0b0110（に対応したベクトル）になっていることがわかります。 なお、当然ながら途中式で出てくる足し算は1ビットの整数同士の足し算として処理しています。

これで1ビットの左シフトを定義することが出来ましたが、2ビットや3ビットのシフトはどうなるでしょうか？ 少し考えると、2ビット左シフトは \[ L_2 := \begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} \] 3ビット左シフトは \[ L_3 := \begin{bmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} \] であるとわかります。 要するに、nビット左シフトの場合には、対角項から右上に n 個だけずれた場所に 1 を書き込んだ行列ということです。 また、実は以下の関係も成り立ちます。 \[ L_2 = (L_1)^2, \quad L_3 = (L_1)^3 \] 一般に \[ L_n = (L_1)^n \] です。 証明は、もちろん実際に行列の掛け算をしてみる（より厳密には帰納法を使う）ことでも示せますが、 ある整数 x を 1 ビット左シフト（$L_1x$）してから、更に 1 ビット左シフト（$L_1(L_1x) = (L_1)^2x$）したものが、 もとの整数 x を 2 ビット左シフトしたもの（$L_2x$）と同じになることは直感的には明らかですので、まぁ自明でしょう。

同様に1ビットの右ビットシフトは \[ R_1 := \begin{bmatrix} 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \] と表されます。 n ビットの右ビットシフト $R_n$ も左ビットシフトの場合と同様で、対角項から左下に n 個だけずれた場所に 1 を書き込んだ行列で、 $R_n = (R_1)^n$ なる関係が成り立ちます。

余裕のある読者は、記事末尾にある「理解度確認テスト » ローテートを表す行列」にもぜひチャレンジしてみてください。

xorshiftの基本演算のベクトル表現

さて、以上で xorshift のアルゴリズムを数学的に取り扱う準備が出来ましたので、 冒頭に掲載した xorshift32 のアルゴリズムを上で解説した行列やベクトルを用いた表現に変換してみましょう。

xorshift の基本的な操作は、以下のようなものです。 なお、次のコードでは左シフトを用いていますが、右シフトの場合も同様の議論が成り立ちます。

冒頭の xorshift32 のアルゴリズムは上の処理をシフト数やシフトの方向を変えながら、 三回施すというものでした。

それでは、この xorshift_atomic という処理をベクトル表現に直してみましょう。 まずビットシフト部分は a ビットの左ビットシフトを表す行列 $L_a$ を用いて、 \[ \text{[ y $\ll$ a のベクトル表現 ]} = L_a y \] と書けます。 さらに、XOR はベクトル同士の足し算で表現できますから、一般に整数 z, w に対して \[ \text{[ z ^ w のベクトル表現 ]} = z + w \] が成り立ちます。 従って、z = y, w = y<<a と思えば \[ \text{[ y ^ (y $\ll$ a) のベクトル表現 ]} = y + (L_a y) \] となります。 さらに単位行列 $I$ を用いると \[ \text{[ y ^ (y $\ll$ a) のベクトル表現 ]} = y + L_a y = (I + L_a) y \] とも書くことができます。

これにより、xorshift の基本的な処理である xorshift_atomic は数学的な表現では $I + L_a$ という行列によって表されることが分かります。

xorshift32のベクトル表現

最後に、記事の冒頭にあった xorshift32（以下に再掲）のベクトル表現を求めてみましょう。

まず、一行目の y ^ (y << 13) の計算結果は \[ (I + L_{13}) y \] となることは既に述べたとおりです。 続いて二行目の y = y ^ (y >> 17) は、普通に考えると $(I + R_{17}) y$ となりますが、 プログラム上では二行目の y は一行目の計算結果を表していますから、y を一行目の出力結果である $(I + L_{13}) y$ で置き換えて、 \[ (I + R_{17}) \left[ (I + L_{13}) y \right] = (I + R_{17}) (I + L_{13}) y \] がこのコードの二行目までの計算結果です。 三行目の計算結果も二行目と同様に考えて \[ (I + L_{15}) (I + R_{17}) (I + L_{13}) y \] ですので、これが xorshift32 という関数の最終結果（戻り値）となります。

まとめると、行列 T を \[ T := (I + L_{15}) (I + R_{17}) (I + L_{13}) \] とおくと、xorshift32 は入力されたベクトルに行列 T を掛け算する処理であると表現することができます。

以上で xorshift32 というアルゴリズムの数学的な記述に関する解説は終わりです。 いよいよ当初の目的であった xorshift32 の周期を調べたいと思いますが、その前に非常に大切な性質の一つとして「行列 T の可逆性」について言及しておきたいと思います。

xorshiftの数理

行列Tの可逆性

乱数生成に用いる行列 T が可逆である（逆行列をもつ）ことは非常に重要です。 なぜならば、行列 T が可逆であれば、出力される乱数が一様であることが保証されるからです。 これは直感的には明らかで、変換行列が可逆であるということは入力された数値を適当に「回転」させるという作用のみを持つということですから、 入力値が一様であれば出力値も当然一様となります。 （行列の可逆性と出力される乱数の一様性の証明は「理解度確認テスト » 乱数生成に用いる行列の可逆性と、出力値の一様性」を参照してください）

例えば左シフトを表す行列 $L_1$ は可逆ではありませんが、$L_1$ の出力値の上位 1 ビットは必ず 0 となってしまいますから、 先頭が 1 となっているような数値は出力されないということになり、一様性が崩れてしまっているのは明らかです。 更に悪いことに、$L_1$ を何回か施しているうちに必ず出力値は 0 になってしまいますので、これではとても行列 $L_1$ を用いて作った数列は擬似乱数列とは言えませんね。

ですので、行列 T がきちんと一様性を担保するような「良い性質」を持つことを保証するために、行列 T の可逆性を示しましょう。

まず行列 T は \[ T = (I + L_{15}) (I + R_{17}) (I + L_{13}) \] と三つの行列の積に分解されていますので、$I + L_{15}, I + R_{17}, I + L_{13}$ それぞれの行列が可逆であれば行列 T も可逆となります[6]。 従って一般に $I + L_a$ が可逆であることを示せば十分でしょう。（$I + L_a$ の可逆性が示せれば $I + R_a$ の可逆性も同様に示せます）

$I + L_a$ の可逆性の証明は簡単で、逆行列を具体的に示すだけです。 \[ I + L_a + L_{2a} + L_{3a} + \cdots \] という行列を考えます。 ここで注意して欲しいのは、この式は一見すると無限に続いているように見えますが、行列が表現している整数のビット数（行列の次元と同じ）を n とすると、 n ビット以上シフトをすると必ずゼロになりますから、$x \geqslant n$ に対しては $L_x$ は零行列となることから、必ずこの式は有限個の足し算で止まります。

この行列に対して $I + L_a$ を掛け算してみると、 \[ \begin{align} (I + L_a + L_{2a} + L_{3a} + \cdots) (I + L_a) & = (I + L_a + L_{2a} + L_{3a} + \cdots) I + (I + L_a + L_{2a} + L_{3a} + \cdots) L_a \\ & = (I + L_a + L_{2a} + L_{3a} + \cdots) + (L_a + L_{2a} + L_{3a} + L_{4a} + \cdots) \end{align} \] となります。 ここで最後の式変形では $L_{ia} L_a = L_{(i+1)a}$ を用いました。

さて、いま行列の各要素は 1 ビットの整数としていますから、全く同じ行列を二個足し合わせると零行列となります。 なぜなら、全く同じ行列を足し合わせるということは行列の各項では全く同じ数字同士を足し合わせるため、 計算結果の行列は 0 + 0 または 1 + 1 が並ぶことになりますが、0 + 0 = 0 となるのは明らかですが 1 + 1 も 1 ビット整数の世界では桁溢れを考慮して 0 となるため、 結局行列の項はすべて 0 になってしまうからです。

この事実を用いると、上の式の一番目のカッコ内の i 番目の項と二番目のカッコ内の i-1 番目の項は互いに打ち消し合って消えてしまい、 最終的には一番目のカッコ内の単位行列 I しか残らないことが分かります。 \[ \begin{align} (I + L_a + L_{2a} + L_{3a} + \cdots) (I + L_a) & = (I + L_a + L_{2a} + L_{3a} + \cdots) + (L_a + L_{2a} + L_{3a} + L_{4a} + \cdots) \\ & = I + (L_a + L_a) + (L_{2a} + L_{2a}) + (L_{3a} + L_{3a}) + \cdots \\ & = I \end{align} \] これにより $I + L_a$ の逆行列は \[ (I + L_a)^{-1} = I + L_a + L_{2a} + L_{3a} + \cdots \] であることが分かります。 なお、右辺は無限に続くように見えますが、有限個の項のみで打ち切られることは既に述べたとおりです。 $I + L_a$ の逆行列が具体的に求まりましたから $I + L_a$ は可逆であり、このことから $I + L_a$（および $I + R_a$）を組み合わせた行列 T も可逆であり、 このことから行列 T を用いて生成した乱数は必ず一様となることが保証されます。

乱数の周期と行列の位数

少し脇道にそれてしまいましたが、いよいよ本題の xorshift アルゴリズムの周期性を計算しましょう。

数学的な準備として、まずは生成される擬似乱数の周期性と、行列の位数について解説します。

さて、いきなり「位数 (order)」という聞き慣れない単語が出てきましたが、行列の位数とは何かというと、 「その行列を何回掛け算したら単位行列になるか？」のことを意味します。

例えば \[ V := \begin{bmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ \end{bmatrix} \] という行列を考えます（これは計算機的にはビット列の反転を表します）。 この行列を 2 回かけると \[ V \times V = I \] と単位行列になりますから、「行列 V の位数は 2」となります。

一方、 \[ V’ := \begin{bmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \end{bmatrix} \] という行列は、 \[ V’ \times V’ = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \] \[ V’^2 \times V’ = \begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ \end{bmatrix} \] \[ V’^3 \times V’ = I \] と、4回掛け算してはじめて単位行列になるため、「V’ の位数は 4」となります。

行列の位数と乱数の周期に関して次の定理が成り立ちます[1]。

定理1（乱数の周期と行列の位数）

T を可逆な n ビットのバイナリ行列とする。 このとき、任意のゼロでない n ビットの初期値 y に対して $y, Ty, T^2y, \cdots, T^{2^n-1}y$ という数列が $1, 2, \cdots, 2^n-1$ の並び替えになるための行列 T のみたすべき必要十分条件は、 行列 T の位数が $2^{n}-1$ となることである。

少し厳密な書き方をしてしまいましたが、要するに「どんなシード値 y を使ったとしても、生成される乱数が $1, 2, \cdots$ を適当に並べ替えたような、非常に性質の良いものになるためには、乱数を作るために使っている行列 T の位数がちょうど $2^n-1$ であればいいし、逆に行列 T の位数が $2^n-1$ じゃなかったら必ず出力値に重複が出来てしまって性質の良い乱数にはならない」ということを言っています。

生成された連続する $2^n – 1$ 個の乱数が $1, 2, \cdots, 2^n-1$ の並び替えになっていれば、明らかに乱数の周期は $2^n-1$ 以上ですから、 この定理は乱数の周期についての保証を与えているとみることが出来ます。 つまり、乱数の周期を調べるためには行列 T の位数を調べればよい、ということです。 また、シード値は 0 でなければどんな値であってもいいのですから、運悪く性質の悪いシード値を選んでしまい、生成される乱数の周期が短くなってしまうような不運は起きないことも保証してくれています。

乱数の周期の保証を与えるためには行列 T の位数を調べればよいのですから、行列の位数が $2^n-1$ かどうかを調べる方法を考えましょう[7]。

行列の位数の判定方法

さて、乱数の周期を調べるためには行列の位数が $2^n – 1$ かどうかを調べれば良いと分かったわけですが、 ここでは少し一般的に、与えられた行列 T の位数が N かどうかを判定するアルゴリズムを考えましょう。

まず定義に従えば \[ T^N = I \] ですので、実際に行列 T を N 乗してみて単位行列になるかどうかをチェックすれば良さそうですが、実はこれだけでは不十分です。 なぜならば、N よりも小さな値 N’ を位数として持っているにもかかわらず、たまたま N’ よりも大きな N に対しても $T^N = I$ という式が成り立ってしまっているだけかもしれないからです。 要するに、$T^N = I$ をチェックしただけではこの $N$ が本当にこの式を満たす最小の整数かどうかは分かりません。

それではどうすればいいかというと、行列 T を一つずつ掛け算しながら $T^2, T^3, \cdots, T^{N-1}$ を順番に求め、 これらが単位行列 I でないことをチェックし、最後に $T^N$ が単位行列になることをチェックすれば良さそうですね。

……しかしながら、この方法には大きな欠点があります。 いま、判定したい位数 N は $2^n-1$ といった非常に大きな値ですから、N 以下の全ての数に対して判定するのは非常に長い時間がかかってしまい、現実的には不可能です。

N 以下の全ての数に対して判定を行うのは現実的ではありませんから、何らかのフィルタリングを行って $T^{N’} = I$ となりそうな N’ の候補を絞ってあげる必要があります。 繰り返し自乗法といったアルゴリズムを用いれば $T^{N’}$ を求めること自体は比較的簡単ですから、N’ の候補をせいぜい 10 個くらい[8]に絞れれば計算できそうです。

そこで、位数に関する以下の定理を利用しましょう。

定理2（位数の性質）

行列 T の位数を N とする。このとき、ある整数 M に対して $T^M = I$ が成り立つのであれば、M は N の倍数である。

証明は練習問題とします（理解度確認テスト » 「位数の性質」の証明）。

もしも $T^N = I$ であるにもかかわらず N’ < N なる N’ に対して $T^{N’} = I$ が成り立っていたとしても、 この定理によれば必ず N は N’ の倍数であることがいえます。 逆に $T^N = I$ かつ $T^{N’} = I$ をみたすような N’ < N は必ず N の約数ですから、 この事実を用いれば N’ の候補をある程度フィルタリング出来そうです。 つまり、N’ の候補として N の約数のみを調べれば十分です。

命題1（位数がNであるための必要十分条件）

行列 T の位数がちょうど N であるための必要十分条件は、$T^N = I$ をみたし、かつ、N の全ての約数のうち N を除いたもの $N_1, N_2, \cdots$ に対して $T^{N_1} \neq I, T^{N_2} \neq I, \cdots$ が成り立つことである。

従って、次のようなアルゴリズムで行列 T の位数が N であるかどうかを効率的に判定することができます。

さて、このアルゴリズムでも十分実用的ではありますが、もう少し効率的なアルゴリズムにすることもできます。 具体的には、上記のアルゴリズムでは N のすべての約数 $N’$ に対して位数となっていないか（$T^{N’} = I$ となっていないか）の判定を行っておりますが、これをかなり省略することができます。

いま N を素因数分解して N = pqr と3個の素数 p, q, r の積で表されたとします。 すると、N の約数としては 1, p, q, r, pq, qr, pr がありますが、 もし $T^p = I$ であったとすると $T^{pq} = (T^p)^q = I^q = I$ となりますから、N’ = p, q, r に対して $T^{N’} = I$ のチェックをしなくても、 N’ = pq, qr, pr のチェックだけを行えば十分であると分かります。

この事実を用いると、次のようにアルゴリズムを改善することができます。

見た目はほとんど変わっていませんが、factors(N) の返す配列の長さ（Nの素因数の数）は divisors(N) の返す配列の長さ（Nの約数の数）と比べて圧倒的に少ないですから、かなりの改善となっています。

優良パラメータの計算

以上で xorshift32 と呼ばれる次のアルゴリズム:

の生成する乱数の周期を計算する方法が分かりました。

具体的には、この関数を行列の形で表現し \[ \underbrace{(I + L_{15}) (I + R_{17}) (I + L_{13})}_{T} {\ } y \] この行列 T の位数が $N = 2^{32}-1$ であるかどうかを以下のアルゴリズム:

でチェックすればOKです。

以上ではすべて擬似コードで示していましたが、以下に実際に動作する Python3 の計算コードを示します。

このコードでは、行列の各行の要素（1ビット整数）32個を連結し、32ビット長の整数値として表現しています。 一つの行列はこの32ビット長の整数値を32個分（32行分）集めた一次元配列となっています。 もちろん、行列を1ビット整数が 32×32 個集まった二次元配列で表現してもいいのですが、 計算がかなり遅くなってしまいますので計算効率のためにこのように行列を表現して計算しています（ので、少し見にくいですが許してください）。

さて、これで冒頭に掲げた xorshift32 というアルゴリズムの周期が確かに $2^{32}-1$ という非常に長い周期を持つことを（数学と計算機の力を借りて）示すことができました。 ところで、コードの中に出てきた (15, 17, 13) という謎のパラメータは別にこの組み合わせでなくとも構いません。 上記の Python3 コードの xorshift32_test の引数の a, b, c をいろいろと弄りながら試してもらえると分かりますが、 実は (15, 17, 13) 以外にも条件をみたすパラメータはいっぱい（全部で81通り）あります[1]。

この「優良パラメータ」をすべて洗い出す問題を作りました（理解度確認テスト » 優良パラメータの計算）ので、余裕のある読者はぜひチャレンジしてみてください。

最後に

発展的な話題

xorshift32 というアルゴリズムの周期を計算するだけでかなりの分量の記事となってしまいましたが、 全6ページあるxorshiftのオリジナルの論文[1]のうち、本記事で解説した周期の話は実は2ページ目までしかありません。 それ以降のページでは64ビットなど、よりビット数の多いアルゴリズムの作り方の紹介であったり、 xorshift32 のように単純に XOR とビットシフトを施しただけでは乱数の性質はあまり良いとは言えず、 いくつかの乱数テストに失敗してしまうことから最終結果の整数乱数に定数を足す改良案が提案（xorshift*）されていたりなど、 さまざまな議論がなされていますので、興味のある方はぜひ調べていただければと思います。

また、xorshiftのオリジナルの論文に触発されて様々な改良が提案されております。 例えば Mersenne Twister の発明者でもある松本氏および斎藤氏による XORSHIFT-ADD (XSadd) や、 それを更に改良した、Vigna氏による xorshift+[2] などがあります。

また実は、Google Chrome の JavaScript エンジン V8 で実際に採用されたアルゴリズムは本記事で解説を行ったオリジナルの xorshift ではなく、xorshift+ の方となっています。 しかしながらアルゴリズムの基本的な考え方であったり必要とされる数学的な前提知識などはほとんど共通ですので、 xorshift をきちんと理解することができればその改良版のアルゴリズムである xorshift+ などの理解も容易かと思います。 （興味のある方は「理解度確認テスト » xorshift128+の行列表現」を解いてみてください）

V8で採用されたアルゴリズム

すぐ上で述べたとおり、Google Chrome の JavaScript エンジン V8 で実際に採用されたアルゴリズムは xorshift を改良した xorshift+ の128ビット版 (xorshift128+) となっております。 せっかくですので、xorshift128+ のアルゴリズムを以下に示します（処理の分かりやすさと見やすさのため、実際のコードの最適化を外したコードを示します）。

xorshift32 とは少し処理が違っていますが、ビットシフトとXORの組み合わせで実現されているところはかなり似ていることが見て取れると思います。

なお、V8 がアルゴリズムを xorshift に切り替える使われていたアルゴリズムは multiply-with-carry (実際に使われている実装は、二つの変数から16ビットずつ取り出して繋げる構造のため、MWC1616 と呼ばれています) と呼ばれる、線形合同法を進化させたようなものとなっております。

二つの処理を比べると、古い方（後者）がコードの行数的には短いものの、途中で乗算が必要となりますので計算コスト的には（CPUにもよりますが）xorshift128+ の方が低いと言えるでしょう[9]。

おわりに

本記事では XOR とビットシフトを組み合わせた y^(y<<a) と言った形の非常にシンプルな演算を数回行うだけで生成できる数列が非常に長い周期を持つことを、 XOR やビットシフトを行列・ベクトル演算と対応付けることで数学的に解析する方法を示しました。 また、計算を行うためのアルゴリズムや実際に動作する Python3 によるコードを示し、パラメータを適切に選ぶことで確かに任意のシード値に対して非常に長い周期をもった乱数列が生成されることも確認しました。

xorshift は他の乱数生成アルゴリズムと比較するとかなり新しいものですが、従来のアルゴリズムと比べて数学的な背景がしっかりとしていることや、 処理が非常に簡単で高速に計算できること、また実装も容易である（コードや演算回路が非常に短く済む）こと、 内部状態のビット長を増やす（これはすなわち、乱数の周期を増やすことにつながる）ことが比較的容易であることなどから、 今後 Google Chrome に限らず採用が進んでいくのではないかと予想されます。

ところが、しっかりと xorshift の数学的な背景を理解するためには比較的高度な数学的知識が要求されますので、 本記事が xorshift の背後で使われている数学理論を理解するための手助けとなったことを願っています。

理解度確認テスト

本記事の内容をきちんと理解できたかどうかをチェックするための問題を作りましたので、余裕のある読者はぜひチャレンジしてみてください。

答えはありませんので、どうしても詰まってしまった場合には周囲の友人に聞いてみるか、 著者宛 (Twitter: @visvirial) に相談をしていただければヒントを差し上げます。

なお、★の数は難易度を表しています。 すべての問題が解けたら xorshift マスター(?)を名乗ってもいいと思います！

☆☆☆ ローテートを表す行列

1 ビットの左および右ローテート（シフトでは追い出されたビットは単純に消えてなくなりますが、ローテートでは反対側にくっついて復活します）を表す行列を求めてください。

☆☆☆ 優良パラメータの計算

本文中に掲載した Python3 コードを用いて、xorshiftの論文の2ページ目下部にある優良パラメータの一覧表を再現してください。

なお、論文の表の一番下の左から三番目に、本記事で用いた xorshift32 のパラメータ (13, 17, 15) があるのが分かるかと思います。

★☆☆ 乱数生成に用いる行列の可逆性と、出力値の一様性

行列 T を n ビットの変換を表す可逆な行列とします。 このとき、n ビット整数 y を $0 \sim 2^n-1$ から一様にランダムに選んだ時に、その出力 $z = T y$ も $0 \sim 2^n-1$ の中で一様に分布することを示してください。

★★☆ xorshift128+の行列表現

xorshift128+ は、結果を出力する際に二つの内部状態整数を足し算する部分を除けば、 本記事で解説を行った行列やベクトルを用いた表現として表すことができます。

そこで、xorshift128+ 関数を一回呼んだ際に state0 および state1 がどのように変換されるのかを表す行列を求めてください。

★★☆ 位数の性質

本文中の定理2「位数の性質」を証明してください。

定理2（位数の性質; 再掲）

行列 T の位数を N とする。このとき、ある整数 M に対して $T^M = I$ が成り立つのであれば、M は N の倍数である。

ヒント（マウスで選択して反転すると見れます）： $T^N, T^{N+1}, \cdots$ は $I, T, T^2, \cdots, T^{N-1}$ を用いてどのように表せるでしょうか？

★★★ 114,514,114,514番目の乱数

xorshift32 の 64 ビットへの拡張である、以下の xorshift64 に対して、この関数を 114,514,114,514 回呼び出した直後の戻り値（つまり、114,514,114,514 番目の乱数）を求めるプログラムを作ってください。

なお、言うまでもないと思いますが、素直にループを回していたら一生かかっても終わらないと思いますので（アルゴリズム的な）何らかの工夫をする必要があります。 （参考までに、筆者の作った Python3 コードではラズパイで 1.1 秒くらいでした。Core i5 だと 0.1 秒くらい）

※ちなみに答えは十進数表記で 8,132,099,081,512,959,504 です。

参考文献

  1. G.Marsaglia, Xorshift RNGs, Journal of Statistical Software Vol. 8 (Issue 14), 2003.
  2. S.Vigna, Further scramblings of Marsaglia’s xorshift generators, arXiv:1404.0390, 2014.

脚注：

  1. 内部状態が一番初めに戻らず、例えば初期状態から100回乱数を生成した状態に戻る、というものもあるかもしれませんが、ここでは説明の簡便さのために「一番初め」としています ↩
  2. もちろん、周期が長いだけで良い乱数であるということはできません。例えば 1, 2, 3, … と単調に増えていく数列は周期こそ長いですが、全くランダムではありませんね ↩
  3. というか、これだけ周期が長いと一生どころか、宇宙年齢くらい経ってもすべての乱数を使い切ることは不可能っぽいですね…… ↩
  4. 最大周期は $2^{32}$ ですので、「『ほぼ』最も長い」としています。ただ、$2^{32}=4294967296$ と $2^{32}-1=4294967295$ の差は僅かですので、気にするほどの誤差ではありません ↩
  5. ここでの説明ではMSBを1行目にする、という作法を採用していますが、もちろんLSBを1行目にするという作法を採用してもOKです ↩
  6. なお、「可逆な行列の積が可逆であること」は、行列 A, B を可逆な行列とすると行列 AB の逆行列は $B^{-1} A^{-1}$（※一般的に $A^{-1} B^{-1}$ とは限りません。念の為）であることから従います ↩
  7. なお、[1]の中にも行列の位数の調べ方が括弧内に書いてあるのですが、説明が不十分で判定をするための条件が一つ抜けていますので、論文を読む際には注意してください ↩
  8. N’ の候補の数は n の値が大きければ大きいほど当然多くなりますので、正確には $O(log(N))$ （やその多項式）程度であることが必要となるでしょう。しかしここでは表現の分かりやすさのために「10個」という具体的な数字を出してしまっています ↩
  9. ただ、MWC1616 の方も大した処理は行っていませんので、実パフォーマンスではどちらもほとんど同じになると思われます ↩