条件分岐をスマートに！『Merkle化抽象構文木 (MAST)』の全貌

（推定読了時間：15分50秒）

最近、Bitcoin のブロックチェーンの肥大化が大きな問題として取り沙汰されることが増えてきました。ブロックチェーンにはジェネシスブロック（一番最初のブロック）から現在に至るまですべてのトランザクションのデータが蓄積されておりますので、 Bitcoinのユーザ数が増えトランザクションが増えていくとともにこの問題は加速していくものと考えられています。そのため、ブロックチェーン肥大化問題は Bitcoin コミュニティ内でもかなり優先度の高い懸案事項として認識されており、様々な改善策が提案されています。

そんな中でサイズ削減の一つの手法として、トランザクションに複雑な条件が記載されている場合にサイズを劇的に削減することのできる画期的なアイディアが提案されました。この手法はMerkle化抽象構文木 (Merkelized Abstract Syntax Tree; MAST) と名付けられているのですが、その名前からも分かる通りBitcoin本体でも利用されている^[1]Merkle木の仕組みを利用しています。

この記事では MAST を理解するために必要な Bitcoin でのトランザクションの仕組みを復習しつつ、MAST の基本原理やメリット・デメリットなどを考察しています。

なお、読者は Bitcoin の基本的な仕組み (拙著連載ブログ記事『暗号通貨ってなんだろう？』相当) を理解しているものと仮定しています。

1 復習：Bitcoinにおけるコイン使用可否判定方法
2 復習：P2SHトランザクション
3 分岐のあるプログラム
4 アイディア
5 Merkle木
6 ネストした分岐
7 所感
- 7.1 Pros.
- 7.2 Cons.
8 まとめ
9 理解度確認テスト
10 参考文献

復習：Bitcoinにおけるコイン使用可否判定方法

Bitcoinでは、未使用のコインを誰が使用できるのかを判定するプログラムをトランザクション内にBitcoinの独自言語（「スクリプト」と呼ばれます）を用いて直接書き込むという、非常にユニークな仕組みを取り入れています。例えば、 アドレスA 宛にコインを送付する際には以下のようなプログラムをトランザクション内に直接書き込みます。

# 入力されたパラメータがあらかじめ関数内に組み込まれているアドレス値に対応する電子署名データかどうかをチェックする関数。
# hash() は適当なハッシュ関数 (Bitcoinのリファレンス実装ではRIPEMD160とSHA256を組み合わせたもの)。
var check_address_A = function(signature, pubkey) {
  # アドレスAの値をプログラム中に直接書き込んでおく。
  const address = 'アドレスA (公開鍵Aのハッシュ値)';
  # 入力された公開鍵のハッシュ値がアドレスAと等しいか検証する。
  if(hash(pubkey) != address) return false;
  # 入力された電子署名が正しいか検証する。
  return checksig(signature, pubkey);
};

# 入力されたパラメータがあらかじめ関数内に組み込まれているアドレス値に対応する電子署名データかどうかをチェックする関数。

# hash() は適当なハッシュ関数 (Bitcoinのリファレンス実装ではRIPEMD160とSHA256を組み合わせたもの)。

var check_address_A = function(signature, pubkey) {

# アドレスAの値をプログラム中に直接書き込んでおく。

const address = 'アドレスA (公開鍵Aのハッシュ値)';

# 入力された公開鍵のハッシュ値がアドレスAと等しいか検証する。

if(hash(pubkey) != address) return false;

# 入力された電子署名が正しいか検証する。

return checksig(signature, pubkey);

};

このような形をしたプログラムは「pay-to-pubkey-hash (P2PH)」と呼ぶのですが、これは上記のプログラムは「公開鍵のハッシュ値を取った値を関数内に組み込んでおき、送金時にはこれと照合する」という処理に相当するからこのように呼ばれているのです。

そして、この アドレスA 宛に送られたコインを使用する際には、使用者が アドレスA の所有者である証明として、このプログラムが true を返すようなパラメータ、すなわち アドレスA に対応する公開鍵と電子署名をトランザクション内に含めます。

var proof_A = {'アドレスAに対応する電子署名', 'アドレスAに対応する公開鍵'};

1 2	var proof_A = {'アドレスAに対応する電子署名', 'アドレスAに対応する公開鍵'};

前者のコイン使用可否判定プログラム check_address_A は公開鍵暗号系における公開鍵のような役割を果たしますので scriptPubKey、後者の二つ組のデータ proof_A は電子署名のような（一方のデータは電子署名そのものなので紛らわしいですが……）役割を果たしますので一般的に scriptSig と呼ばれています。

渡されたトランザクションが正しいか検証する場合には、トランザクション内に含まれている scriptSig というデータを、使用しようとしている（すでにブロックチェーンに取り込まれている、未使用の）トランザクションに含まれている scriptPubKey という関数に適用した結果を見る、ということをします。

このようにコイン使用可否判定プログラム scriptPubKey をトランザクション内にわざわざ含めるのは非常にまどろっこしいですし、トランザクションのデータサイズも大きくなってしまいますので一見無駄のように見えますが、一方で任意の処理を記述することができますので非常に柔軟にコインの使用可否条件を記述することができます。このような仕様のおかげで後方互換性をある程度保ちながらマイクロペイメントチャネルやマルチシグのような仕組みを導入することができたということを強調しておきます。

復習：P2SHトランザクション

Bitcoin開発当初は上記の仕組みで運用されていたわけですが、このように「送金先」として任意のプログラムを含むことを許すといくつか不都合な点が発生します。そのうちの一つとして、送金先を「アドレス」で指定できなくなるということがあります。送金先の「プログラム」が check_address_A で示したような pay-to-pubkey-hash 型のプログラムに固定されていれば、 アドレスA の情報を送金先のアドレスとして扱い、受け取ったアドレスをもとに check_address_A と同様のプログラムを作成すれば問題ありませんが、それ以外の複雑なプログラムを送金先として指定したい場合にはプログラムの長〜いリストを（送金者にプログラムのテキストデータをメールで渡すなどして）送金先として指定してもらわなければなりません。これではあまりにも不便だ（それ以外にも理由はありますが、個人的にはこれが最も大きな理由だと感じています）ということで考えられたのが pay-to-script-hash (P2SH) という仕組みです (BIP16)。

簡単に説明すると、送金先とするプログラムを直接記述するのではなく、最初はそのハッシュ値のみを格納した scriptPubKey を指定しておき、コインの使用時にプログラムの引数とともにプログラムの本体データを scriptSig として指定する、ということをします。

これを具体的にみていきましょう。まず送金時には以下のようなプログラムを指定します。

var pay_to_script_hash = function(data, script) {
  const scriptHash = 'スクリプトのハッシュ値';
  if(hash(script) != scriptHash) return false;
  return script(data);
};

var pay_to_script_hash = function(data, script) {

const scriptHash = 'スクリプトのハッシュ値';

if(hash(script) != scriptHash) return false;

return script(data);

};

要するに、送金時に送金してもらう相手にプログラムを指定してもらうのではなく、受け取ったコインを使うときにはじめて自分でプログラムを指定するようにするのです。

一方、このコインを使用する際には、以下のようなデータを scriptSig として指定します。

var proof = {
  '引数',
  function(data) { (送金先として指定したかったプログラムをここに記載) }
};

var proof = {

'引数',

function(data) { (送金先として指定したかったプログラムをここに記載) }

};

例えばマルチシグトランザクションの場合には1番目には「電子署名」を、2番目には「マルチシグを検証するプログラム」をそれぞれ指定します。

こうすることで「スクリプトのハッシュ値」をアドレスとみなせば、長〜いプログラムをわざわざ指定することなく簡単に送金先を指定することができるようになります。また、誰かが実際に送金を行うためにトランザクションを作成するまでは proof の二番目の値であるプログラムの中身は誰にも分かりませんので、プライバシー的にもこちらの方が好ましいことが分かるでしょう。

ちなみにマルチシグを利用したことのある読者は、送金先アドレスが通常の 1... ではなく 3... という形になっていることに気づいていることと思います。これは、1... というアドレスは pay-to-pubkey-hash 型のプログラムに、3... というアドレスは pay-to-script-hash 型のプログラムにそれぞれ対応していることを示しています。（なお、pay-to-pubkey-hash 型でも pay-to-script-hash 型のプログラムでもないような送金先の場合には「送金先アドレス」は定義されていません。というか、この二つのどちらの型とも一致しないプログラム宛に送金したい場合には基本的には pay-to-script-hash の仕組みを使うことが推奨されています。）

分岐のあるプログラム

入力されたパラメータに応じて分岐をさせ違う処理を走らせる、というのはプログラミングの際によく出てくる方法だと思います。 Bitcoinのスクリプトにもこのような機能は存在しており、支払いチャネル周りを中心として使われ始めています。

その一つの例として以下に「Aさん、もしくはBさんが使用できる」というトランザクションを示します^[2]。なお、既に述べた P2SH の仕組みを使うことを前提として scriptSig のみを記載しています。

# Aさん、もしくはBさんが使用できるトランザクションに対応するP2SHスクリプトの擬似コード
#
# @param user 誰がこのトランザクションを使用しようとしているかを表す整数。0ならAさん、それ以外ならBさん。
var check_a_or_b = function(int user, string signature, string pubkey) {
  const addrA = 'Aさんのアドレス (公開鍵のハッシュ値)';
  const addrB = 'Bさんのアドレス (公開鍵のハッシュ値)';
  if(user == 0) {
    # 入力値がAさんの署名だと仮定して署名検証を行う
    if(hash(pubkey) != addrA) return false;
    return checksig(signature, pubkey);
  } else {
    # 入力値がBさんの署名だと仮定して署名検証を行う
    if(hash(pubkey) != addrB) return false;
    return checksig(signature, pubkey);
  }
}
var params = {
  0,  // Aさんのアドレスに対して検証するように指示する
  signatureA, pubkeyA  // Aさんの秘密鍵から作った電子署名および公開鍵
};
var scriptSig_a = { params, check_a_or_b };

# Aさん、もしくはBさんが使用できるトランザクションに対応するP2SHスクリプトの擬似コード

# @param user 誰がこのトランザクションを使用しようとしているかを表す整数。0ならAさん、それ以外ならBさん。

var check_a_or_b = function(int user, string signature, string pubkey) {

const addrA = 'Aさんのアドレス (公開鍵のハッシュ値)';

const addrB = 'Bさんのアドレス (公開鍵のハッシュ値)';

if(user == 0) {

# 入力値がAさんの署名だと仮定して署名検証を行う

if(hash(pubkey) != addrA) return false;

return checksig(signature, pubkey);

} else {

# 入力値がBさんの署名だと仮定して署名検証を行う

if(hash(pubkey) != addrB) return false;

return checksig(signature, pubkey);

}

var params = {

0, // Aさんのアドレスに対して検証するように指示する

signatureA, pubkeyA // Aさんの秘密鍵から作った電子署名および公開鍵

};

var scriptSig_a = { params, check_a_or_b };

言うまでもありませんが、送金時には上記の check_a_or_b （をシリアライズしたデータ）のハッシュ値をアドレスとする pay_to_script_hash 関数を scriptPubkey として指定し、送金されたコインを利用する場合には上記の scriptSig_a を scriptSig としたトランザクションを生成します。

さて、Aさんが上述の check_a_or_b を利用しているコインを使用しようとするトランザクションを作成し、そのトランザクションを検証することを考えましょう。このとき check_a_or_b の後半の処理である B さんのアドレスに対して電子署名の検証を行うコード (L12-14) は一切実行されません。また一度利用したコインは二度と利用することはできませんから、 check_a_or_b の後半の処理は一生実行されることのない、非常に無駄なデータであることが分かります。

このように二度と実行されることのない無駄なデータをトランザクションに含まなくとも済むように考えられた仕組みが Merklized Abstract Syntax Tree (MAST) になります^[3]。

アイディア

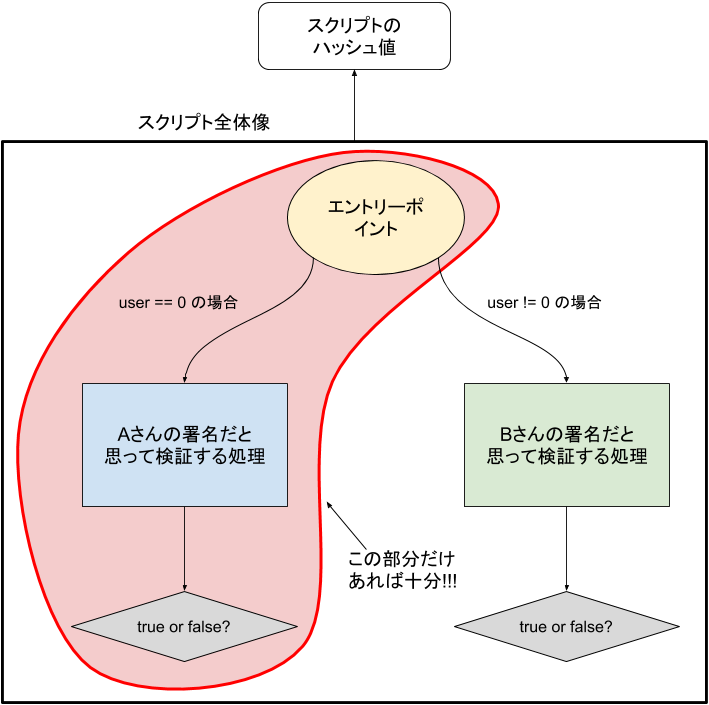
さて、まずは思考を整理するために上述のプログラム check_a_or_b を図示してみましょう。

概ね上のような図がかけると思います。すでに述べたとおり、図右下の「Bさんの電子署名だと思って検証する処理」は不要で、赤色で囲った領域のプログラムさえあれば十分です。ならば単純に赤枠のプログラムだけを P2SH トランザクションのスクリプトとして採用すれば良いのではないか、と思うかもしれませんが実はこれではダメです。なぜならば、左下の処理が不要なのか右下の処理が不要なのかはこのトランザクションを使用するときにはじめて分かることであり、トランザクション作成時にはどの部分が不要なのかは確定していないからです。そうするとトランザクション作成時に含める「スクリプトのハッシュ値」としては、処理を省略せずに全部書いたプログラムに対してハッシュ値をとったものを採用するしかなく、その結果送金時にハッシュ値チェックに合格するためには、（たとえ一部処理が実行されないことがわかっていても）すべての処理を記述したプログラムを指定してあげなければならないことになります。

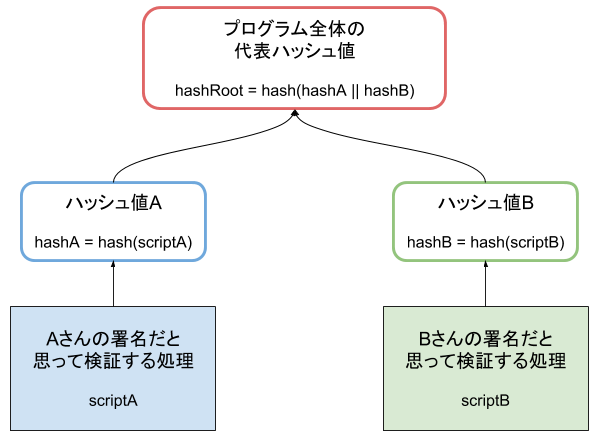
ですので従来通りの仕組みですと不要だとわかっていてもすべての処理を記述しないわけにはいかなかいのです。そこでこの問題を克服するために、単純にスクリプト全体のハッシュ値を計算するのではなく、プログラムのパーツごとにハッシュ値を計算しそれらの値を集計するようにしてみましょう。

このような構造にすれば、プログラム全体（scriptA + scriptB）ではなく、scriptA + hashB だけを指定すればプログラム全体の代表ハッシュ値 hashRoot を再現することができますので、これをもって送金時の P2SH ハッシュ値チェックに合格できそうです。 scriptB の代わりに hashB を利用することで、scriptB の長さが長ければ長いほどデータ量を削減できそうだということが分かると思います。

Merkle木

さて次に分岐処理が大量にある場合を考えてみましょう。この場合、単純に hashRoot = hash(scriptA || scriptB || scriptC || ...) というふうに代表ハッシュ値を計算しても良いのですが、このような処理を見て何か思い出さないでしょうか……？

ブロックにどのトランザクションが含まれているのかの情報を保持するのに、ビットコインでは Merkle 木という仕組みを利用していたことを思い出してください。トランザクションのハッシュ値の配列をそのままブロック内に含めるのではなく、二分木を用いて計算した「トランザクション全体の代表ハッシュ値（Merkleルート、といわれる）」を保持しておくことでトランザクションが含まれているかどうかを高速に判定できるようにしていたのでした。（※詳しくは拙著連載記事暗号通貨ってなんだろう？⑦「第五部『その他』」を参照してください。）

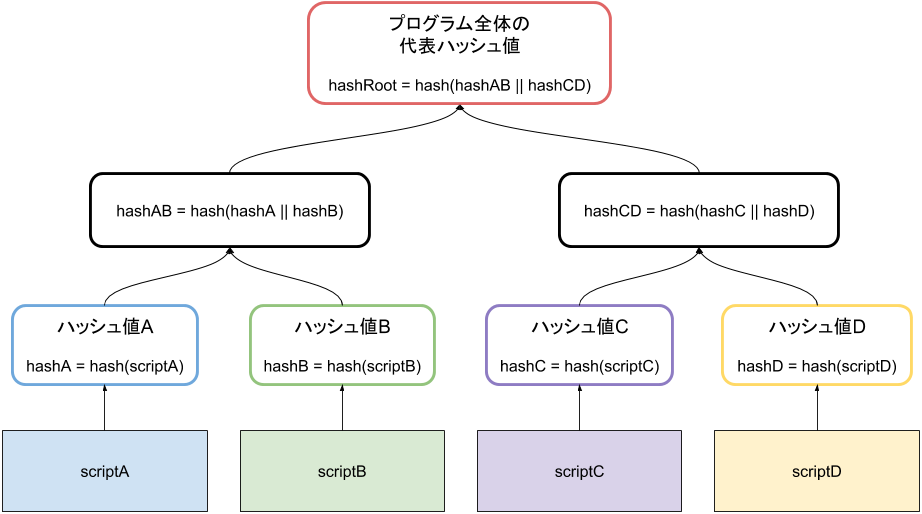
今回もこれと同じような仕組みが使えそうです。例えば分岐先が四つのプログラムの場合には以下のようにすれば良さそうです。

このような構造をとることで、分岐先が $N$ 種類とすると高々 $O(\log(N))$ 個のハッシュ値を提示するだけで Merkle ルートの値の検証ができるようになるでしょう。これにより、特に分岐数が膨大な場合にサイズ削減効果は甚大なものとなることが分かると思います。

この効果を示す顕著な例としてBIP草稿[1]で示されている「巨大なマルチシグトランザクション」を紹介しておこうと思います。例えば 3-of-2000 のマルチシグトランザクションを作ろうとした場合には、トランザクション内に 2,000 個のアドレスをすべて含まなければならず、とてもではないですが現実的ではありません。（アドレス一つが約20バイトですので、最低でも 40KB は必要となります。）このトランザクションは、2,000 個のアドレスから三つのアドレスを選び出すすべての組み合わせを網羅し、これらを条件分岐でつなげることで 1,331,334,000 個の 3-of-3 マルチシグを集めたものとして表現することができます。ですので、MAST の仕組みを使えばトータルで $\log_2(1,331,334,000) \simeq 30.31$ 程度のオーダーのデータ量で済ますことができるということが分かります。その結果、トランザクション全体のサイズは 1.5KB 以下の大きさまで削減することができるのです！なお、これに関して練習問題をいくつか用意しましたので余裕のある読者は挑戦してみてください。

ネストした分岐

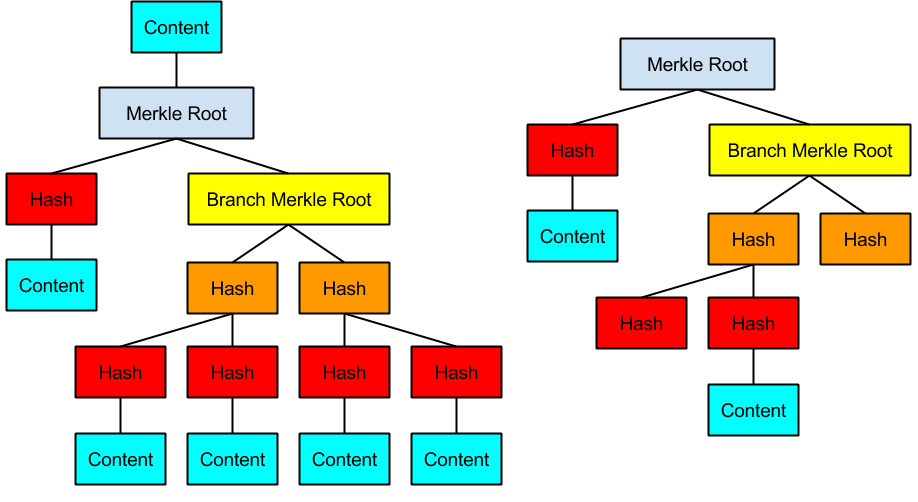
ここまでは分岐が一番最初に一回しか行われておらず、また分岐の前後には処理が一切無い場合を議論してきました。しかしながら木構造を拡張することでもっと複雑な条件分岐処理を表現することも可能です。その一例として示されているのが MAST の論文[2]に示されている以下の図の左側です。

この図がどのような形のプログラムに対応するのかについては、練習問題としておきます。

所感

Pros.

ほぼ副作用なしに導入できる（ソフトフォークで導入可能であり、オーバヘッドによるサイズ増大等はほとんどない）ため、かなり良さそう
特に複雑な条件分岐を伴うトランザクションを作成する場合に効果を発揮するため、支払チャネルまわりで出てくる複雑なトランザクションを（サイズをあまり気にせず）気軽に利用できるようになるかも
実装は思ったよりも簡単ぽい（BIP草稿[1]にあるものは40行程度の追加で済む）
Ethereum のスマートコントラクト等にも応用できそう

Cons.

現時点（2016年4月）では条件分岐を多用した複雑なトランザクションが用いられることはほとんどなく、導入されたとしても少なくとも現時点ではサイズ削減効果は限定的だと思われる

まとめ

本記事では、Bitcoin のスクリプトに条件分岐が多用されている場合には、 Merkle木の仕組みをうまく使うことでスクリプトの一部をトランザクション内部にわざわざ含めなくともスクリプトの一部のハッシュ値のみを含めば、安全性を保ちながらも大幅なデータ削減効果が見込めることを説明しました。また、上記の仕組み「Merkle化抽象構文木 (Merkelized Abstract Syntax Tree; MAST)」を理解するために必要な、Bitcoinのスクリプトシステムの概要も併せて説明しました。

理解度確認テスト

【☆☆☆】1,331,334,000個のマルチシグ

本文中で「3-of-2000 のマルチシグは、1,331,334,000 個の 3-of-3 マルチシグで表現することができる」と書きました。 1,331,334,000 という数字をどのように導き出したのかを説明してください。

【★☆☆】MAST論文の図に対応するプログラム

MAST論文[2]で紹介されている下図左側の木に対応するプログラムを書き下してください。

【★★☆】check_a_or_bのスクリプト表現

「Aさん、もしくはBさんが使用できる」トランザクションとして挙げた check_a_or_b という処理をBitcoinのスクリプト言語を用いて書きなおしてください。

【★★★】2-of-3 マルチシグのMAST表現

本文中で 3-of-2000 のマルチシグを分解して MAST 表現に直す、という話がありましたがこれは具体的にどのようにやるのでしょうか？さすがに 3-of-2000 ですと数があまりにも膨大となってしまいますので、ここでは 2-of-3 マルチシグの MAST 表現を考えてみてください。

本文中に示したような擬似コードで変換結果を示してください
Bitcoinのスクリプト言語を用いて変換結果を書き下してみてください

参考文献

[1] Johnson Lau, Merkelized Abstract Syntax Tree (MAST導入に関するBIPの草稿) [2] J.Rubin, M.Naik and N.Subramanian, Merklized Abstract Syntax Tree

脚注：

Merkle木は、トランザクションがブロックに含まれていることを高速に確認できるように利用されています (c.f. 簡易版支払検証/Simplified Payment Verification; SPV)。 ↩
これは機能的にはいわゆる「マルチシグ」と同等のトランザクションです。通常はマルチシグトランザクション用の命令 OP_MULTISIGVERIFY を利用しますが、ここでは説明のためにあえて分岐命令を用いた特殊なトランザクションを使っています。 ↩
論文を読むとビットコインに限らず一般的に利用できるような雰囲気で一応書かれていますが、ビットコイン向けに考案された仕組みであることは明らかです。 ↩