Diffie-Hellmanの鍵交換(Diffie-Hellmanの鍵共有、または省略してDH鍵交換またはDH鍵共有)とは、現在よく知られているいわゆる「公開鍵暗号体系」のアイディアのベースとなったもので、 盗聴の可能性のあるネットワーク(通信路)を通して二人が共通の秘密(共有秘密)を安全に交換するアルゴリズムです。
秘密を交換する最も単純な方法は、二者のうちどちらか一方が秘密を作成し、それをもう片方に送付することですが、 この方法だと途中にいる盗聴者により秘密が盗まれてしまう可能性があります。 そのため、DH鍵交換では両者が秘密を「半分づつ出し合って」最後にそれぞれが受け取った秘密情報を合体させ、秘密を作成する、という方法を取っています。
DH鍵交換は1976年に発明されてから40年近く経ちますが、現在でもSSLなどで広く使われている方式となっています。
歴史を含めた詳細はWikipediaの記事に譲るとして、 ここではDH鍵交換のアルゴリズムを図を使って簡単に解説します。
群論の基礎知識を前提としています。
離散対数問題
なぜか日本語版のWikipediaでは触れられていませんが、DH鍵交換が安全である根拠として、「離散対数問題」を解くのが非常に難しい(と信じられている)ということがあります。
離散対数とは、通常の対数(log)を離散的な群に対して適用したもので、以下のように定義されています。 すなわち $G$ を有限巡回群としたとき、生成元 $g \in G$ およびある元 $a \in G$ に対して \[ g^n = a \] を満たす整数 $n$ が必ず存在します($\because \text{$g$ が生成元だから}$)。この $n$ を求める操作(函数)のことを離散対数といいます。
通常の対数との類似性からこの函数を \[ n = \log_g(a) \] と書きます。
離散対数問題とは、この離散対数を効率的に求めることが一般的には非常に難しい、という問題です。 $g^n$ を求めるのは繰り返し自乗法を用いることで $n$ の桁数と同一のオーダ $O(\log(n))$ で計算できますが、 この逆問題である離散対数に関しては繰り返し自乗法のように指数的な効率で計算する手法は知られておらず、 $n$ の桁数に対して指数的な時間のかかるアルゴリズムしか知られていません。
素因数分解は「素数同士を掛け算するのは非常に高速にできるが、掛け算した結果を素因数分解し、元の素数を求めるのは非常に難しい」という性質を持ち、 この性質はRSA暗号の安全性の根拠となっていることはよく知られていますが、 これと同様にこの離散対数問題の難しさは今回の記事で紹介するDH鍵交換を含むいくつかの暗号アルゴリズムの安全性の根拠となっています。
なお、言うまでもないかもしれませんが群構造が自明な場合には離散対数の計算が簡単な場合もあります。 例えば加法群 $(\mathbb{Z}/n\mathbb{Z})$ については $(\mathbb{Z}/n\mathbb{Z}) \ni i = \underbrace{1 + \cdots + 1}_{i}$ ですから、 $\log_1(i) = i$ となります。
アルゴリズム
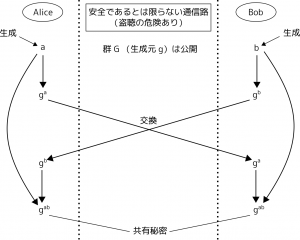
AliceとBobが、途中に盗聴者がいるかもしれない通信路を通して、共通の秘密情報を交換しようとしている状況を考えます。
$G$ を巡回群とし、$g$ をその生成元とします。
このとき、AliceとBobはそれぞれ次のような手順で秘密を共有します。
- 共有する秘密の半分に相当する秘密情報の作成
- Alice: 整数 $a$ を生成
- Bob: 整数 $b$ を生成
- 公開情報の作成と送信
- Alice: $g^a$ を計算し、Bobに送信
- Bob: $g^b$ を計算し、Aliceに送信
- 共有秘密の計算
- Alice: Bobからもらった公開情報と、Aliceの持つ秘密情報を組み合わせ、共有秘密 $s_a := (g^b)^a$ を計算
- Bob: Aliceからもらった公開情報と、Bobの持つ秘密情報を組み合わせ、共有秘密 $s_b := (g^a)^b$ を計算
ここで明らかに $s_a = g^{ab} = s_b$ ですから、これにより共通の秘密 $s_a = s_b =: s$ を交換することができたと分かります。
考察
さて、このときに盗聴者が共有秘密 $s$ にアクセスするのは本当に難しいのでしょうか? このことを見るために、盗聴者が知りうる情報をリストアップしてみます。
- 群 $G$ および生成元 $g$
- AliceからBobに送った公開情報 $g^a$
- BobからAliceに送った公開情報 $g^b$
一見、$g^a$ と $g^b$ を掛け算すると共有秘密が再現できてしまいそうですが、$g^a \cdot g^b = g^{a+b} \neq g^{ab} = s$ ですので、微妙に違います。
他に色々と試してみても、$a$ または $b$ の情報のうちどちらか一方がなければ共有秘密は再現できなさそうだ、ということが解ると思います。



otaky
-Diffie-Hellmanの鍵交換について勉強しています。
いろいろなサイトを見ていましたが、このサイトはとてもわかりやすかったです。
ただこのDiffie-Hellmanの鍵交換での安全への理解ができない箇所なのですが、
生成元g、公開情報g^a,g^b が分かると、g^x=g^a g^x=g^b
とxを変えていけばすぐに,a,bってわかるんではと思ってしまいます。
どう理解したらよいでしょうか。
びりある
-すみません、返信がかなり遅くなってしまいました。
ご質問についてですが、これはまさに離散対数問題の困難性の話でして、例えば https://blog.visvirial.com/articles/721#i-3 などをご覧いただければと思います。
『縮約(縮退)自然数』
-≪…離散的な群に対して適用したもの…≫ではないのですが、『離散的有理数の組み合わせによる多変数創発関数論 命題Ⅱ』の[多変数]と[量化係数](孵化係数)との[組み合わせ]で[暗号化]を出来るかどうか、研究される人はいないでしょうか?