さて次に、どのようにブロックチェインデータの改ざん（以前のデータを書き換えてしまうこと）を防ぐのかについて解説します。

もしも簡単に改ざんが出来てしまうと、一旦正常に支払を済ませ、商品またはサービスをもらった後に自己の支払トランザクションを改ざんし、 なかったことにすることで支払を一方的にキャンセルできてしまいますから、改ざんができないようにすることは非常に重要です。

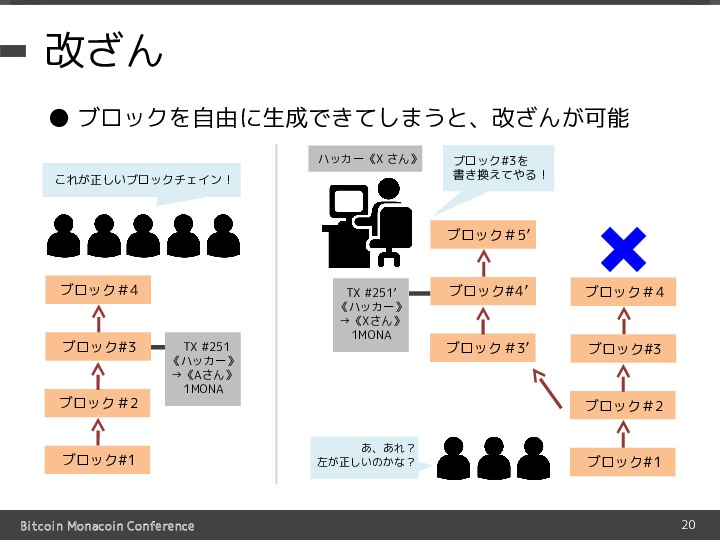
先ほど解説を行ったブロックチェインの仕組みでは、誰もが自由にブロックを生成できてしまうとすると、 図で示したようにキャンセルを行いたい自己のトランザクションが含まれているブロックの一つ手前のブロックから、 新しいブロックチェインを分岐させ、既存のブロックチェインよりも長いものを作るということが容易に出来てしまいます。

すると、ネットワークは最も長いブロックチェインを正当なものとみなしますから、既存のブロックチェインが無効であるとみなされ、 攻撃者の生成した新たなブロックチェインが正当であると認識されてしまいます。 この新たに差し替えられたブロックチェインに最初の支払トランザクションではなく、送金先を自分や友人の保有するアドレスに書き換えたトランザクションを含むことで最初の支払トランザクションを無効化し、 一旦支払ったコインを自分や友人のものにすることが出来てしまうのです。

一つ前のスライドでみたように、誰もが自由にブロックを生成できてしまうと比較的簡単に改ざん（支払トランザクションのキャンセル）ができてしまいますので、 ブロック生成に何らかの制約を加えないといけないことが分かります。

それでは具体的にどのような制約を加えればいいのでしょうか？

すぐに思いつくのは参加ノード全員でくじ引き（ここで個々のノードはIPアドレス一つにつき一ノードとします）を行い、ブロックを生成できるノードを決めることです。 このようにすれば、悪意のあるノードが既存のブロックチェインを超える長さの新しいブロックチェインを生成するのは、よほどの運がない限り不可能となるからです。

ところがこの方法ですと、攻撃者が大量のIPアドレスを確保できてしまう（例えばISPなどの事業者や、ボットネットを利用できる者など）場合には投票権を高い確率で独占できてしまいますので、 あまり公平な方法であるとはいえないでしょう。

そこでBitcoinが提案をしたのは、IPアドレスひとつにつき一票を与えるのではなく、いわば「CPU一個あたりに一票を与える」といったものです。 このようにすれば、大量のCPUを保有し運用するためには大量の設備費と電気代が必要となりますので、IPアドレスを一人で独占するよりは遥かに難しそうであると考えられます。

では、具体的に「CPU一個につき一票」を実現するにはどのようにしたらいいのでしょうか？

それには自己の保有する計算能力を不正が出来ない形で第三者に示すことができれば十分であると考えられますが、 実はこのような方法は「プルーフ・オブ・ワーク（Proof of Work; PoW）」と呼ばれ、以前から知られていました。

そこで、これから数スライドに渡ってPoWについてもう少し詳しくみていくことにします。

「CPU一個につき一票」を実現するためには、まず大量の計算コストが必要な問題を用意し、 それを一番初めに解けた人が勝者となってブロックを生成できるようにすればよさそうです。

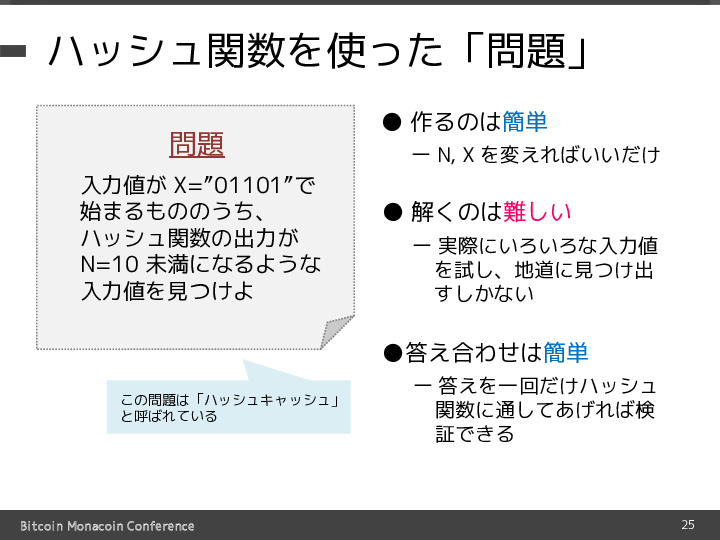
ここで用意する「問題」としては、まずそもそも問題を作るのが難しいとそこで処理が詰まってしまいますから、①問題を作るのは簡単でなければいけません。 一方、大量の計算コストが必要なことが要求されますので、②解くのは難しいことも要求されます。 最後に、もし誰かが問題を解けたとしても、解答者が提示した答えが本当に正しい答えなのかどうかをすぐさま判定できないといけませんから、③答え合わせは簡単でなければいけません。

このような三つの条件を揃えた問題にはどのようなものがあるのでしょうか？

前のスライドで示した三つの性質が備わっている問題として、まず一つ身近な例としてはパズルゲームがあげられます。

例えばルービックキューブでは適当に面を回転させることで比較的容易に問題は作れますから「①問題をつくるのは簡単」はクリアできます。 ですが、解くのが難しい^[1]のはパズルゲームである以上自明ですから、「②解くのは難しい」もクリアできます。 一方で実際にどのようにキューブを動かせば解けるのか、という答えを示してもらえればその答えが正しいかどうかは実際にキューブを回していくことで容易に確かめることができますから、 「③答え合わせが簡単」もクリアできます。

さて、確かにこのようにパズルゲームはこの三つの性質を備えていることが分かりましたが、コンピュータ上でルービックキューブを回すのは明らかに不効率ですので、 もう少しコンピュータに適した問題はないのでしょうか？

実は「ハッシュキャッシュ」と呼ばれる問題があり、この問題は上の三つの性質を兼ね備えています。 ハッシュキャッシュの説明に入る前に、ハッシュキャッシュの理解に非常に重要な「ハッシュ関数」と呼ばれるものについて、次のスライドで簡単にみてみましょう。

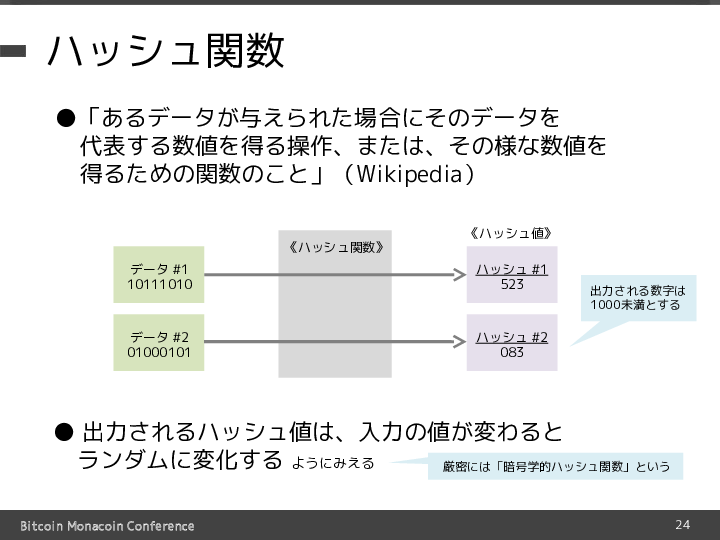
ハッシュ関数とは「あるデータが与えられた場合にそのデータを代表する数値を得る操作、または、その様な数値を得るための関数のこと」とWikipediaでは解説されています。

少し難しいですが、要するに与えられたデータをハッシュ関数と呼ばれるものに通すと、適当に変換されてランダムな数字が出てくる（ただし、出てくる数字の上限は決まっている）もの、と考えればOKです。

なお、出力される数字は入力値が少しでも違うとランダムに変化します^[2]が、同じ入力値であれば必ず同じ出力値になることに注意してください。

ちなみに、暗号処理でハッシュ関数を用いることがよくあるのですが、このようなランダム性などの性質が弱いと暗号化が不十分となってしまうことがあります。 そのため、暗号処理に適した性質がきちんと備わっているハッシュ関数のことを特別に「暗号学的ハッシュ関数」ということがあります。 暗号通貨でもこのような性質が重要となる場面がありますので、これは暗号通貨にとっても非常に重要な性質と言えます。

このハッシュ関数を用いた問題として「ハッシュキャッシュ」と呼ばれている、スライド左側の問題を考えましょう。 この問題が先程述べた三つの性質を兼ね備えているかどうかをみていきます。

まず、様々な問題を作るためには図中のNやXを変更するだけでいいため、「①作るのは簡単」は容易にクリアできそうです。

次に「②解くのが難しい」ですが、これは入力値を変えると出力される数値がランダムに変わっていってしまいますから、 目的の数値を見つけるためにはひたすら入力値を変えながら計算してみるしかありませんので、これもクリアできそうです。

最後に「③答え合わせが簡単」ですが、これもひとたび答えを見つけることができれば、 その答えを実際にハッシュ関数に通してあげることで本当に正しい出力値が出てくるのかどうかを容易に確かめることが出来ますので、 クリアできそうです。

以上の考察により、確かにこのハッシュキャッシュと呼ばれる問題は、目的の性質をすべて備えていることが分かりました。

ちなみにハッシュキャッシュの「キャッシュ」を英語で書くと「cash」すなわち「お金」という意味になります。 データを一時的に取り出しやすい場所に置いておくことを表す「cache」ではありませんので注意してください。

しかしなぜ「お金」なのでしょうか？

ハッシュキャッシュはそもそもメールスパムを防止するために考えだされました。 メールを送信するときには必ずこのハッシュキャッシュの問題を解かなければならない、というルールを課すことができれば、 一通のメールを送るのにある程度のCPU時間（計算能力）を消費しなければいけなくなりますので、 大量に様々な宛先に向けてメールを送信しまくる、というのが非常に難しくなり、スパムメールを減らすことができると考えられたためです。 これは直感的には「計算能力を（お金のように）支払わないと、メールが送れない」と捉えることが出来ますので、 cash（お金）という言葉が使われたようです。

ただ、現時点でハッシュキャッシュがメールシステムで使われることはほとんどありません。 現時点でのハッシュキャッシュのメインユーザはBitcoinとなっていますので、 1997年にハッシュキャッシュが提案されてから約十年経ち、ようやく実用的な使われ方が見つかり、陽の目をみることができた、といった感じでしょうか。

さて、Bitcoinから少し外れた話題が続きましたが、ここからまたBitcoinの仕組みの話に戻ります。

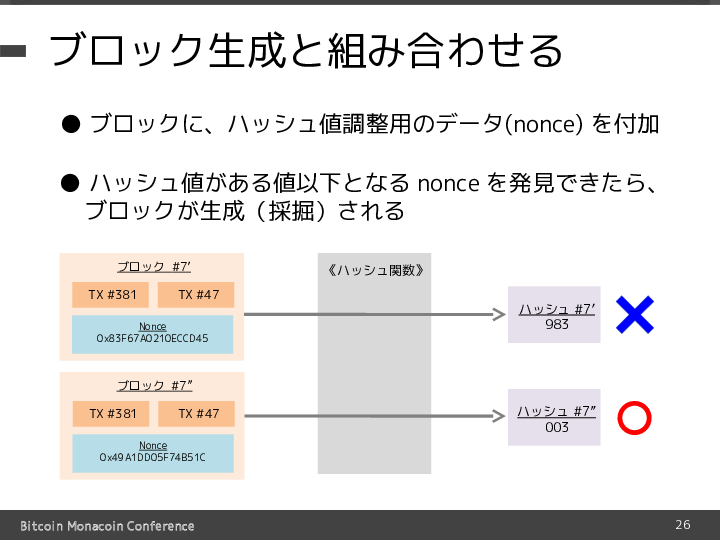
暗号通貨のブロック生成の仕組みの中で、このハッシュキャッシュはスライドの図のように使われています。 すなわちブロック内にトランザクション以外にハッシュ値調整用の「nonce（ナンス）」と呼ばれるデータ領域を新たに設け、 このnonce値を色々と変えながら目的のハッシュ値が出てきたらそのブロックは有効とみなされる、ということをしています。

このようにすることでどのようなメリットが得られるのかを次のスライドでもう一度振り返ってみましょう。

このようにブロック生成アルゴリズムにハッシュキャッシュを組み合わせることで、 ハッシュ値をたくさん計算できる人（多くの計算能力を持つ人）がブロックを生成できる確率が高くなります。

これにより先ほど目標として掲げた「CPU一個につき一票」が実現できていることが分かります。

悪意のあるノードが不正にブロックチェインを伸ばし、元のブロックチェインのデータを上書き（改ざん）するためには、 元のブロックチェインに参加する善良な参加者を上回る速度で不正なブロックチェインを伸ばし、追いつき追い越さなければいけません。 従って、このように計算能力に応じたブロック生成権を与えることで、 参加者全体の計算能力のおよそ過半数の計算能力を持たない限りはこのような改ざん攻撃は非常に難しくなることが分かります。

暗号通貨ではこういった仕組みにより、悪意のあるノードの攻撃からブロックチェインのデータを守っているのです。

さてここで、実際にブロックを採掘するのがどのくらい難しいのか（どのくらいハッシュ値を計算しなければいけないのか）をみてみましょう。

Bitcoinで採用しているハッシュ関数はSHA-256と呼ばれるもので、SHA-256の出力値のとりうる値はおよそ \(0 \sim 1.2\times10^{77}\) です。 一方2014年3月時点で採掘されたブロックのハッシュ値はおよそ \(4.4 \times 10^{54}\) ですから、 出力値が均等にランダムに出てくると仮定すれば、簡単な計算により \(2.6 \times 10^{22}\) 回(!)のハッシュ値を計算しなければなりません^[3]。

どんなに計算効率のいい計算コードを書いたとしても、CPUのクロック周波数よりも多くのハッシュ関数を計算するのは不可能です^[4]ので、多めに見積もったとしても一秒間に \(10^{10}\) 回が限度でしょう。 すると一台のPCで計算を行い、ブロックを発見できるまでの平均時間はおよそ \(2.6 \times 10^{22} / 10^{10} = 2.6 \times 10^{12} \text{秒}\) すなわち8万2,500年(!)となります。

このように現在のBitcoin採掘は既に一般家庭のコンピュータではとても太刀打ち出来ない状況となっており、 Bitcoin採掘専用マシンを大量に並べた「Bitcoin採掘工場」を作らない限り、とてもブロックを発見できるような状況ではないということが分かります。

これまでに説明した範囲では実は二つの大きな問題があります。

ひとつ目は、ブロックを採掘するためには大量の電気代とマシン代が必要となりますが、そこまでして採掘をするモチベーションはなんなのか？という問題です。

もうひとつは、そもそもコインは最初はどこから湧いて出てくるのか？という問題があります。 Bitcoinのトランザクションはコインを人から人へと受け渡す処理でしたが、 そもそも一番最初にコインを手にする人は一体誰なのでしょうか？

これらの課題は、ブロックを実際に採掘できた人に対してコインを報酬として与える、ということで解決できます。 大量の電気代を消費してブロックを採掘したとしても、報酬として電気代以上のコインが貰えるのであれば皆こぞって採掘に勤しむでしょうし、 またこれは同時に、コインの初期配布の手段ともなっています。

なお、このブロック毎に与えられる報酬のことを「ブロック報酬（block reward）」といいます。

---

---